如何提高移液準確度？

簡介移液是當今生命科學實驗室中最常見的活動之一。精確測量和轉移從微升到毫升的極少量液體需要操作員具有良好的移液技術，使用經過校準的移液器並選擇適合任何給定協議的吸頭。因此，將移液視為一個系統是一種始終如一地產生準確結果的行之有效的方法。科學、培訓和不斷的實踐表明，某些技術（例如，吸入角度、吸入和分配速率等）可以提高移液準確性。但什麼是移液準確性？它是如何定義的？它是如何計算的？本文旨在透過提供簡單而清晰的範例並描述「不確定性」一詞及其對移液的影響，以及考慮這種不確定性的重要性，幫助任何移液器使用者理解移液準確性背後的基本概念和數學。

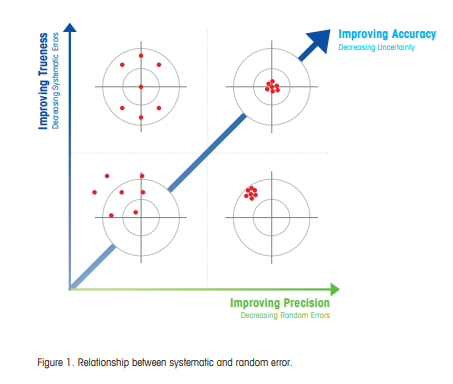
移液精度移液精度衡量移液器使用者提供等於或接近選定體積的液體分配量的能力。分配體積的精度取決於以下因素：

• 與移液器儀器和吸頭相關的誤差
• 樣品中的液體類型（物理和/或化學性質）
• 使用者技術
• 环境影响，例如环境温度和气压
  与移液器仪器和吸头相关的误差
  两种类型的误差会影响单个分配体积的质量：
  系统误差
  在移液术语中，系统误差 (SE) 衡量分配体积与预期体积的接近程度。
  系统误差来自仪器本身（移液器），并且对于每个分配体积都保持相同的值或比例。系统误差的示例包括使用未校准的移液器或使用非标准吸头（例如，加长）。一般而言，系统误差是可预测的，因此可以减少（例如，使用校准的移液器）。系统误差可以定性地描述为“真实度”。
  随机误差
  随机误差 (RE) 是分配体积的可重复性。在移液术语中，随机误差衡量在保持相同实验条件下，相同数量的分配体积彼此之间的接近程度。顾名思义，随机误差是不可预测的，并且对于每个分配体积而言都不相同。
  随机误差的例子包括温度波动和移液技术。随机误差可以定性地描述为“精度”。
  系统误差和随机误差如何影响整体移液精度？精度是系统误差和随机误差的组合（图 1）。

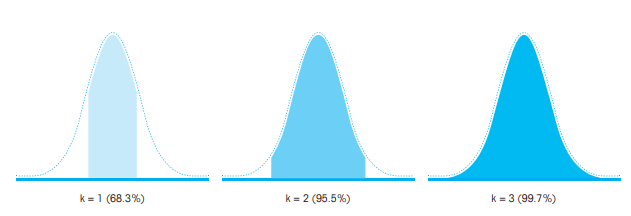
單次分配體積的不確定性原則上，移液器使用者應校正已知系統誤差的測量值。對於移液而言，這意味著需要從每個分配體積中減去系統誤差。此步驟不太實用。相反，「單次分配體積的不確定性」考慮了系統誤差和隨機誤差。它使用以下近似方程式計算，此後縮寫為分配體積的不確定性：分配體積的不確定性(μL) = | 系統誤差| + k * 隨機誤差此方程式用於估計單次分配體積的不確定性，當移液器使用者需要驗證其移液器的性能時很有用。在此方程式中，k 是擴展因子。擴展因子也稱為覆蓋因子，根據定義的標準偏差值確定分配體積的置信度。例如，如果 k = 1，則分配體積的置信度為 68.3%。如果 k = 2，則信賴度為 95.5%，如果 k = 3，則信賴度為 99.7%。實際上，68% 的置信度從未被推薦，因為它允許「太多」錯誤測量（即分配量過低或過高）。另一方面，99% 的置信度太嚴格，幾乎沒有失敗的餘地。在科學協議中，通常接受 95% 的置信度。在移液中，95% 的置信度意味著，如果移液器使用者必須在相同條件下（移液器、吸頭、技術和樣品）分配相同體積20 次，則19 次分配將在可接受的不確定性（置信範圍）內，且只有一個分配體積會被拒絕（即分配量過低或過高）。

解釋移液中的不確定度如果移液器的不確定度為 20 ± 2 µL，則表示移液器使用者確信實際分配的體積在18 至 22 µL 之間。解釋移液不確定度的一種方法是使用者對預期體積與分配體積的接近程度的最佳估計。

根據先前的信息，可以確定覆蓋因子是置信水準的函數。以下範例說明了置信水準和重複次數在估計平均值、標準差和不確定度方面的影響。

移液精度範例一旦確定了系統誤差和隨機誤差，計算移液中的不確定度就相對簡單且易於理解。案例1：標稱量程對移液精度的影響假設使用者想要估計經過校準的Rainin XLS+ L-20 移液器的不確定度，該移液器使用10 次重複（即重複的單次分配量）輸送20、10和2 µL DI 水。遵循製造商針對此特定 20 µL 移液器發布的規格：

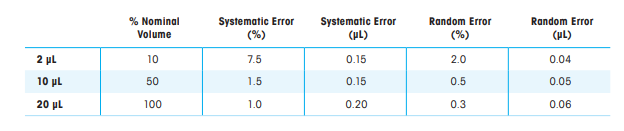
使用不確定度方程式不確定度(μL) = | 系統誤差(μL) | + k* 隨機誤差(μL)然後：如果V = 20 μL，則不確定度= | 0.20 (μL) | + k* 0.06 (μL)如果V = 10 μL，則不確定度= | 0.15 (μL) | + k* 0.05 (μL)如果V = 2 μL，則不確定度= | 0.15 (μL) | + k* 0.04 (μL)如果所需的信心水準為 95%，則分配體積數為 10 (n = 10)，則覆蓋率因子 k = 2。不確定度(20 μL) = | 0.20 (μL) | + 2* 0.06 (μL) = 0.32 μL (1.6%)不確定度(10 μL) = | 0.15 (μL) | + 2* 0.05 (μL) = 0.25 μL (2.5%)不確定性(2 μL) = | 0.15 (μL) | + 2* 0.04 (μL) = 0.23 μL (11.5%)這些結果表明，不確定性與標稱容量有關。當我們將移液器操作得更接近其最大標稱容量 (100% = 20 µL) 時，即使假設置信度較高，相對不確定性也會變得更小。在所給出的範例中，與移液器在10% 標稱容量附近操作時的不確定性相比，置信度為95.45% 的20 µL（100% 標稱容量）的不確定性要小七倍。

如果用戶決定降低置信度，會發生什麼情況？使用相同條件但置信度為 68%，則 k = 1（再次強調，不建議將置信度降低到 68%，因為這會導致給定協議中出現「太多」失敗）。不確定性(20 μL) = | 0.20 (μL) | + 1 * 0.06 (μL) = 0.26 μL (1.3%)不確定度(10 μL) = | 0.15 (μL) | + 1 * 0.05 (μL) = 0.2 μL (2%)不確定性(2 μL) = | 0.15 (μL) | + 1 * 0.04 (μL) = 0.19 μL (9.5%)

比較兩組結果（68% 和 95% 置信度），可以確定不確定性是置信度的函數。置信度越高，不確定性越大。