Introduction Pipetting is one of the most common activities in life science laboratories today. Accurately measuring and transferring extremely small amounts of liquid from microliters to milliliters requires the operator to have good pipetting techniques, use calibrated pipettes and select tips suitable for any given protocol. Therefore, thinking of pipetting as a system is a proven way to consistently produce accurate results. Science, training, and ongoing practice have shown that certain techniques (e.g., aspiration angle, aspiration and dispensing rates, etc.) can improve pipetting accuracy. But what is pipetting accuracy? How is it defined? How is it calculated? This article aims to help any pipette user understand what lies behind pipetting accuracy by providing simple and clear examples and describing the term "uncertainty" and its impact on pipetting, as well as the importance of considering this uncertainty. Basic concepts and mathematics.
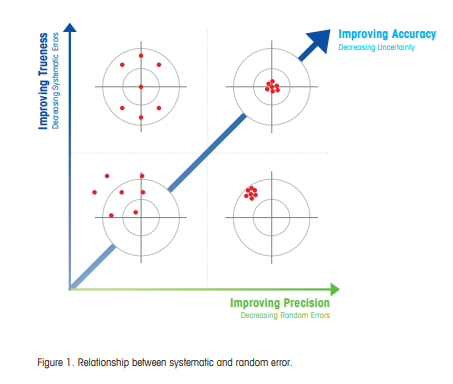
Pipetting Accuracy Pipetting accuracy is a measure of the pipette user's ability to deliver a volume of liquid dispensed at or near a selected volume. The accuracy of the dispensed volume depends on the following factors:
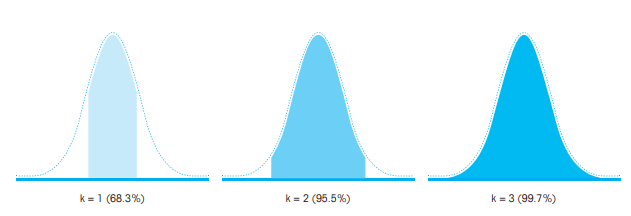
Uncertainty in Single Dispense Volume In principle, pipette users should correct measurements for known systematic errors. For pipetting, this means that the systematic error needs to be subtracted from each dispensed volume. This step is not very practical. In contrast, "uncertainty in a single dispensed volume" takes into account both systematic and random errors. It is calculated using the following approximate equation, hereafter abbreviated as Uncertainty of Dispensed Volume: Uncertainty of Dispensed Volume (μL) = | Systematic Error | + k * Random Error This equation is used to estimate the uncertainty of a single dispensed volume, Useful when pipette users need to verify the performance of their pipettes. In this equation, k is the expansion factor. The spread factor, also known as the coverage factor, determines the confidence in the dispensed volume based on a defined standard deviation value. For example, if k = 1, the confidence in the dispensed volume is 68.3%. If k = 2, the confidence level is 95.5%, and if k = 3, the confidence level is 99.7%. In fact, a 68% confidence level is never recommended because it allows for "too many" false measurements (i.e., the dispensed amount is too low or too high). On the other hand, 99% confidence is too stringent and leaves little room for failure. In scientific protocols, a confidence level of 95% is generally accepted. In pipetting, 95% confidence means that if a pipette user had to dispense the same volume 20 times under the same conditions (pipet, tip, technique, and sample), 19 of the dispenses would be within acceptable Within the uncertainty (confidence range), and only one dispensed volume will be rejected (i.e. dispensed volume is too low or too high).
Interpreting Uncertainty in Pipetting If a pipette has an uncertainty of 20 ± 2 µL, it means that the pipette user is confident that the actual volume dispensed is between 18 and 22 µL. One way to interpret pipetting uncertainty is the user's best estimate of how close the expected volume is to the dispensed volume.
Based on the previous information, it can be determined that the coverage factor is a function of the confidence level. The following example illustrates the impact of confidence level and number of replicates on estimating the mean, standard deviation, and uncertainty.
Pipetting Accuracy Example Once systematic and random errors have been determined, calculating uncertainty in pipetting is relatively simple and easy to understand. Case 1: Effect of Nominal Volume on Pipetting Accuracy Assume that the user wants to estimate the uncertainty of a calibrated Rainin XLS+ L-20 pipette using 10 replicates (i.e., the single dispensed volume of the replicate) Deliver 20, 10, and 2 µL DI water. Follow the manufacturer's published specifications for this specific 20 µL pipette:
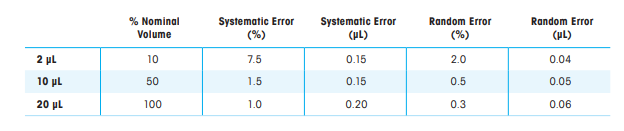
Using the uncertainty equation Uncertainty (μL) = | Systematic Error (μL) | + k* Random Error (μL) Then: If V = 20 μL, then Uncertainty = | 0.20 (μL) | + k* 0.06 (μL) If V = 10 μL, then uncertainty = | 0.15 (μL) | + k* 0.05 (μL) If V = 2 μL, then uncertainty = | 0.15 (μL) | + k* 0.04 (μL) If the desired confidence level is 95% and the number of dispensed volumes is 10 (n = 10), then the coverage factor k = 2. Uncertainty (20 μL) = | 0.20 (μL) | + 2* 0.06 (μL) = 0.32 μL (1.6%) Uncertainty (10 μL) = | 0.15 (μL) | + 2* 0.05 (μL) = 0.25 μL (2.5%) uncertainty (2 μL) = | 0.15 (μL) | + 2* 0.04 (μL) = 0.23 μL (11.5%) These results show that the uncertainty is related to the nominal volume. As we operate the pipette closer to its maximum nominal capacity (100% = 20 µL), even assuming a higher confidence level, the relative uncertainty becomes smaller. In the example given, the uncertainty in 20 µL (100% nominal volume) with a confidence level of 95.45% is seven times smaller than the uncertainty when the pipette is operated around 10% nominal volume. times.
What happens if the user decides to lower the confidence level? Using the same conditions but with a confidence level of 68%, then k = 1 (again, lowering the confidence level to 68% is not recommended as this will result in "too many" failures in a given protocol). Uncertainty (20 μL) = | 0.20 (μL) | + 1 * 0.06 (μL) = 0.26 μL (1.3%) Uncertainty (10 μL) = | 0.15 (μL) | + 1 * 0.05 (μL) = 0.2 μL (2%) Uncertainty(2 μL) = | 0.15 (μL) | + 1 * 0.04 (μL) = 0.19 μL (9.5%)
Comparing the two sets of results (68% and 95% confidence), it is possible to determine the uncertainty as a function of confidence. The higher the confidence level, the greater the uncertainty.
The experienced service team and strong production support team provide customers with worry-free order services.
